Focus Article on : Magdalou, B. (2021). A model of social welfare improving transfers. Journal of Economic Theory, 196.
It is standard practice to assess a country’s economic performance based on its GDP per capita. In the past, GDP has also been used as an indicator of social well-being. However, it is increasingly recognized that social well-being cannot be restricted to a populations’ average income, and that other indicators should be considered. A recent example is the European Commission’s Beyond GDP Initiative, which aims to “develop indicators that are as clear and appealing as GDP, but more inclusive of environmental and social aspects of progress”. [1].
In this paper we assume that the concept of well-being is multidimensional. This may include not only income, but also education level, health status or exposure to air pollution. We also assume that each dimension is measured on a scale with its own measurability requirements. This can be an ordered categorical scale (such as self-reported health status, ranging from “very bad” to “very good”) or a cardinal scale (such as income, measured in money). The only limitation is that this scale is discrete, meaning that it can only have a finite number of possible values. It follows that the situation of an individual can be summarized by an “outcome”, namely a variable indicating the level achieved in each dimension. Finally, a social welfare distribution (of a country for example) compares the number of individuals with each possible outcome.

Photo : Benjamin Disinger / Unsplash
But how can we define the concept of “social progress”? The idea here is to propose criteria allowing pairwise comparisons of social welfare distributions. The most common practice is to use synthetic indices. For example, international organizations usually evaluate income inequality on the basis of the Gini index, ranging from 0 (for a perfectly egalitarian income distribution) to 1 (for a distribution where one person receives all the income). The advantage of such an approach is that the measure is summarized into a single value, which is easily comparable between one distribution and another. The main limitation is that the aggregation of information is extreme, with the risk of having distributions with very close indices but profoundly different characteristics.
In this paper, we approach the definition of social progress from a different perspective. First, we assume that it is possible to define an “elementary transformation of the distribution”, which leads to an unambiguous social welfare improvement. For example, it is usually agreed that an increase in the income of one individual, leaving the situation of all others unchanged, “improves” the distribution of income (the so-called Pareto principle). Similarly, a transfer of income from one individual to another who is relatively poorer is thought to reduce inequality (the Pigou-Dalton principle). If an agreement emerges on a social welfare improving transfer, we can definitively say that one distribution of social welfare dominates another, as soon as the former is obtained from the latter by a sequence of such transfers.
In practice, how can we know if a distribution (obtained with real data) can be derived in this manner from another distribution? A fundamental result in economics and statistics is the Hardy-Littlewood-Polya (HLP) Theorem. This theorem states: It is equivalent to write that one income distribution is obtained from another by a sequence of Pigou-Dalton transfers, or to write that the final distribution dominates the initial distribution according to the Lorenz criterion. The Lorenz criterion is a simple statistical test for understanding income inequality, which associates each p% of the poorest individuals, with their cumulative income share. The graph obtained for any p (ranging from 0 to 1) gives us a curve, called the Lorenz curve. According to the Lorenz criterion, the higher the Lorenz curve, the lower the inequality. The advantage of this approach is to provide a crystal-clear ranking of the distributions if the curves do not intersect. However, such a transparency comes at a price: The criterion is no longer able to rank the distributions if the curves intersect.
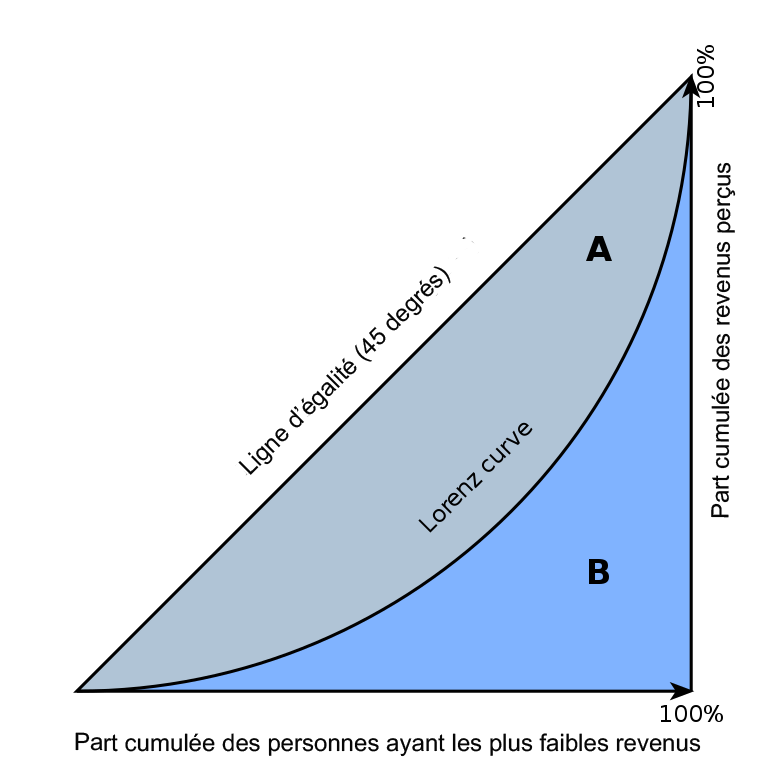
The aim of this paper is to generalize the HLP theorem. This generalisation is abstract, for two reasons. First, individual outcomes can be unidimensional or multidimensional, and each dimension can be cardinal or ordinal. Second, we are not focused on a particular type of welfare-improving transfers (such as Pigou-Dalton transfers), but only impose structural properties on these transfers, namely that: (i) a transfer can be written as the difference between two distributions and (ii) if a transfer is assumed to be welfare-improving, the reverse transfer is welfare-decreasing. This is a flexible definition, encompassing almost all the types of transfers investigated in the literature. From a more formal point of view, a sequence of such transfers has the structure of a “discrete cone”. Our results establish the existence, within this framework, of a simple criterion to compare two distributions (comparable to the Lorenz criterion), thus allowing us to know if one is derived (or not) from the other by a sequence of the transfers in question. Another finding helps us describe how this criterion can be concretely obtained, based on an algorithmic approach.
This paper is methodological and can be used by policy makers as a “toolbox”. The latter is free to define the dimensions he or she considers important to characterize social welfare. Moreover, it is up to him or her to choose the elementary transformations which can be considered as unambiguous social welfare improvements. On this basis, the paper indicates how to obtain the criterion for comparing such distributions. While this paper focuses on the measurement of social welfare, its scope is in fact much broader. It provides a theoretical framework for comparing probability distributions (defined on a discrete support), for example in terms of efficiency, dispersion or risk. Examples of possible alternative applications include: comparing the profitability of financial assets, comparing the performance of machine learning models, or comparing biodiversity loss between different countries.
Notes
[1] Commission Européenne. Qu’est-ce que l’initiative «Au-delà du PIB» https://ec.europa.eu/environment/beyond_gdp/index_en.html




